ML:基礎學習
課程:機器學習基石
簡介:第六講 Theory of Generalization
補滿半邊,然而在對角線上,則為 \(2^N -1\),那麼剩下的呢?
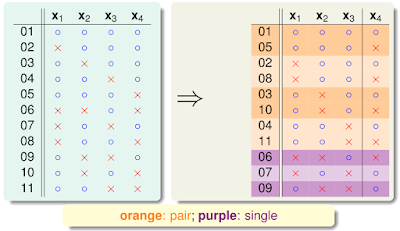
先看 \(B(4,3)\),如下圖,用程式跑出左邊的組合,再分類成右邊
將成雙的定義為 \(2\alpha\) 個,單個的定義為 \(\beta\)
把 \(X_4\) 遮掉來看
因 \(B(4,3)\) 任意三個點不能 shatter,那麼只剩下三個點也不能 shatter,故 \(\alpha+\beta \le B(3,3)\)
此時若只單看橘色的部分,若有兩個點 shatter,此時也會造成 \(B(4,3)\) shatter,故 \(\alpha \le B(3,2)\)
故
得到 \(VC\ bound= 0.298\)
即使是 10000筆資料,錯誤上限機率也有近 30%
課程:機器學習基石
簡介:第六講 Theory of Generalization
Bounding Function
\(B(N,k) = m_H(N)\ 當\ break\ point = k\ 時\)
補滿半邊,然而在對角線上,則為 \(2^N -1\),那麼剩下的呢?
| \(B(N,k)\) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
先看 \(B(4,3)\),如下圖,用程式跑出左邊的組合,再分類成右邊
將成雙的定義為 \(2\alpha\) 個,單個的定義為 \(\beta\)
把 \(X_4\) 遮掉來看
因 \(B(4,3)\) 任意三個點不能 shatter,那麼只剩下三個點也不能 shatter,故 \(\alpha+\beta \le B(3,3)\)
此時若只單看橘色的部分,若有兩個點 shatter,此時也會造成 \(B(4,3)\) shatter,故 \(\alpha \le B(3,2)\)
故
$$
\begin{align*}
B(4,3)&=2\alpha+\beta \\
\alpha+\beta &\le B(3,3) \\
\alpha &\le B(3,2) \\
\Rightarrow B(4,3) &\le B(3,3)+B(3,2) \\
\end{align*}
$$
推導得知
$$
\begin{align*}
B(N,k)&=2\alpha+\beta \\
\alpha+\beta &\le B(N-1,k) \\
\alpha &\le B(N-1,k-1) \\
\Rightarrow B(N,k) &\le B(N-1,k)+B(N-1,k-1) \\
\end{align*}
$$
事實上 \(\le\) 可為 \(=\)
| \(B(N,k)\) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
$$B(N,k)\le\sum_{i=0}^{k-1}\binom{N}{i}$$
2D perceptrons break point = 4
$$
m_H(N) \le \frac{1}{6}N^3+\frac{5}{6}N+1
$$
VC bound
$$
\mathbb{P}\left [ \exists h \in H s.t. \left | E_{in}(h)-E_{out}(h) \right | > \epsilon \right ] \le 2 \cdot \color{Orange}{ m_H(N)}\cdot e^{-2\epsilon ^2N}
$$
若 \(N\) 夠大
$$
\mathbb{P}\left [ \exists h \in H s.t. \left | E_{in}(h)-E_{out}(h) \right | > \epsilon \right ] \le 4 \cdot m_H(2N) \cdot e^{-\frac{1}{8}\epsilon^2N}
$$
所以 2D perceptrons 代入 \(m_H(N) = O(N^3)\) 可收斂之注意:VC bound 是非常寬鬆的上限
例:在 positive rays, \(m_H(N) = N + 1\),\(\epsilon = 0.1\ and\ N = 10000\)得到 \(VC\ bound= 0.298\)
即使是 10000筆資料,錯誤上限機率也有近 30%




留言
張貼留言