[Circuit] S-Parameters (Scattering parameters)

電路知識：S-Parameters (Scattering parameters)
工具：Qucs

簡介：推導與原理

$$ \begin{bmatrix} b_1\\ b_2 \end{bmatrix} = \begin{bmatrix} S_{11} & S_{12}\\ S_{21} & S_{22} \end{bmatrix} \begin{bmatrix} a_1\\ a_2 \end{bmatrix} $$ $$ \begin{matrix} a_1 = \frac{\mathbf{V_1+Z_0I_1}}{2\mathbf{\sqrt{Z_0}}} & a_2 = \frac{\mathbf{V_2+Z_0I_2}}{2\mathbf{\sqrt{Z_0}}}\\ b_1 = \frac{\mathbf{V_1-Z_0^*I_1}}{2\mathbf{\sqrt{Z_0}}} & b_2 = \frac{\mathbf{V_2-Z_0^*I_2}}{2\mathbf{\sqrt{Z_0}}} \end{matrix} $$ $$ \begin{matrix} \left.\begin{matrix} S_{11}=\frac{b_1}{a_1} \end{matrix}\right|_{a_2=0} & \left.\begin{matrix} S_{12}=\frac{b_1}{a_2} \end{matrix}\right|_{a_1=0}\\ \left.\begin{matrix} S_{21}=\frac{b_2}{a_1} \end{matrix}\right|_{a_2=0} & \left.\begin{matrix} S_{22}=\frac{b_2}{a_2} \end{matrix}\right|_{a_1=0} \end{matrix}\\ $$

\(\mathbf{Z_0}\) 為任意值，通常為 50Ω
$$ \begin{align*} a_i &= \frac{\mathbf{V_i+Z_0I_i}}{2\mathbf{\sqrt{\mathrm{Re}[Z_0]}}} \\ b_i &= \frac{\mathbf{V_i-Z_0^*I_i}}{2\mathbf{\sqrt{\mathrm{Re}[Z_0]}}} \\ \\ |a_i|^2 & = a_ia_i^* \\ &= \frac{\mathbf{V_i+Z_0I_i}}{2\mathbf{\sqrt{\mathrm{Re}[Z_0]}}}\cdot \frac{\mathbf{V_i^*+Z_0^*I_i^*}}{2\mathbf{\sqrt{\mathrm{Re}[Z_0^*]}}} \\ &= \frac{\mathbf{V_iV_i^*+V_iZ_0^*I_i^*+V_i^*Z_0I_i+Z_0I_iZ_0^*I_i^*}}{4\mathrm{Re}[\mathbf{Z_0}]}\\ |b_i|^2 & = b_ib_i^* \\ &= \frac{\mathbf{V_i-Z_0^*I_i}}{2\mathbf{\sqrt{\mathrm{Re}[Z_0]}}}\cdot \frac{\mathbf{V_i^*-Z_0I_i^*}}{2\mathbf{\sqrt{\mathrm{Re}[Z_0^*]}}} \\ &= \frac{\mathbf{V_iV_i^*-V_iZ_0I_i^*-V_i^*Z_0^*I_i+Z_0^*I_iZ_0I_i^*}}{4\mathrm{Re}[\mathbf{Z_0}]}\\ |a_i|^2-|b_i|^2 &= \frac{\mathbf{V_iV_i^*+V_iZ_0^*I_i^*+V_i^*Z_0I_i+Z_0I_iZ_0^*I_i^*}}{4\mathrm{Re}[\mathbf{Z_0}]} - \frac{\mathbf{V_iV_i^*-V_iZ_0I_i^*-V_i^*Z_0^*I_i+Z_0^*I_iZ_0I_i^*}}{4\mathrm{Re}[\mathbf{Z_0}]}\\ &= \frac{\mathbf{V_iI_i^*Z_0^*+V_i^*I_iZ_0+V_iI_i^*Z_0+V_i^*I_iZ_0^*}}{4\mathrm{Re}[\mathbf{Z_0}]}\\ &= \frac{\mathbf{V_iI_i^*(Z_0+Z_0^*)+V_i^*I_i(Z_0+Z_0^*)}}{4\mathrm{Re}[\mathbf{Z_0}]}\\ &= \frac{2\mathbf{V_iI_i^*\mathrm{Re}[\mathbf{Z_0}]}+2\mathbf{V_i^*I_i\mathrm{Re}[\mathbf{Z_0}]}}{4\mathrm{Re}[\mathbf{Z_0}]}\\ &= \frac{\mathbf{V_iI_i^*}+\mathbf{V_i^*I_i}}{2}\\ &= \frac{2\mathrm{Re}[\mathbf{V_iI_i^*}]}{2}\\ &= \mathrm{Re}[\mathbf{V_iI_i^*}]\\ \end{align*} $$ 可看出 \(a_i\)、\(b_i\) 的單位其實是 \(\sqrt{power}\)
然而 \(|a_i|^2\) 就像是輸入功率，然而 \(|b_i|^2\) 就像是反射功率
兩者相減後，得到消耗功率
若 \(\mathbf{V_i}\) 和 \(\mathbf{I_i^*}\) 不是 rms 值，而是 max 值
此時需乘上 \(\frac{1}{2}\) 才是真正的功率
原因可參考此篇 [Circuit] AC Sinusoids 穩態分析

傳輸線傳遞的概念，也可以看作能量傳遞
\(S_{11}\)：回波損耗 (return loss)，值越接近 0 越好 (越低越好 ，一般 -25 ~ -40dB)
\(S_{12}\)：反向傳輸增益，值越接近 0 越好
\(S_{21}\)：插入損耗 (inset loss)，或是頻率響應：值越接近 1 越好 (0dB)
\(S_{22}\)：輸出端反射係數，值越接近 1 越好 (0dB)

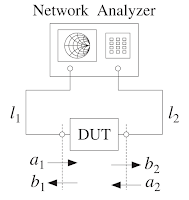
Network Analyzer 原理

$$ \delta _i = \beta l_i\\ S= \begin{bmatrix} S_{11} & S_{12}\\ S_{21} & S_{22} \end{bmatrix} = \left [\begin{array}{ll} S{}'_{11}e^{2j\delta _1} & S{}'_{12}e^{j(\delta _1+\delta _2)}\\ S{}'_{21}e^{j(\delta _1+\delta _2)} & S{}'_{22}e^{2j\delta _2} \end{array} \right ] $$ 令 \(\mathbf{Z_L}=\mathbf{Z_0}\) 則 \(a{}'_2=0\)，可求 \(S{}'_{11}\) & \(S{}'_{21}\)
交換兩邊，可求 \(S{}'_{12}\) & \(S{}'_{22}\)

根據 [Circuit] Transmission line
$$ \begin{align*} \mathbf{V}(z)&=\mathbf{V_f}e^{-\gamma z}+\mathbf{V_r}e^{\gamma z}\\ \mathbf{I}(z)&=\mathbf{I_f}e^{-\gamma z}-\mathbf{I_r}e^{\gamma z}\\ &= \mathbf{\frac{V_f}{Z_0}}e^{-\gamma z}-\mathbf{\frac{V_r}{Z_0}}e^{\gamma z}\\ \mathbf{Z_0I}(z) &= \mathbf{V_f}e^{-\gamma z}-\mathbf{V_r}e^{\gamma z}\\ \mathbf{V_f} &= \frac{\mathbf{V}(z)+\mathbf{Z_0I}(z)}{2}e^{\gamma z}\\ \mathbf{V_r} &= \frac{\mathbf{V}(z)-\mathbf{Z_0I}(z)}{2}e^{-\gamma z} \end{align*} $$ 當 \(z=0\)
$$ \begin{matrix} a_1 = \frac{\mathbf{V_1+Z_0I_1}}{2\mathbf{\sqrt{Z_0}}}=\frac{\mathbf{V_{1f}}}{\mathbf{\sqrt{Z_0}}} & a_2 = \frac{\mathbf{V_2+Z_0I_2}}{2\mathbf{\sqrt{Z_0}}}=\frac{\mathbf{V_{2f}}}{\mathbf{\sqrt{Z_0}}}\\ b_1 = \frac{\mathbf{V_1-Z_0^*I_1}}{2\mathbf{\sqrt{Z_0}}}=\frac{\mathbf{V_{1r}}}{\mathbf{\sqrt{Z_0}}} & b_2 = \frac{\mathbf{V_2-Z_0^*I_2}}{2\mathbf{\sqrt{Z_0}}} =\frac{\mathbf{V_{2r}}}{\mathbf{\sqrt{Z_0}}} \end{matrix} $$ 假設為無損耗傳輸線
$$ \begin{align*} \gamma &= j\beta\\ \\ \begin{bmatrix} a{}'_1\\ b{}'_1\\ \end{bmatrix} &= \begin{bmatrix} \frac{\mathbf{V{}'_1+Z_0I{}'_1}}{2\mathbf{\sqrt{Z_0}}}\\ \frac{\mathbf{V{}'_1+Z_0I{}'_1}}{2\mathbf{\sqrt{Z_0}}}\\ \end{bmatrix}\\ &= \begin{bmatrix} \frac{\mathbf{V{}'_1+Z_0I{}'_1}}{2\mathbf{\sqrt{Z_0}}}e^{\gamma (-l_1)}e^{-\gamma (-l_1)}\\ \frac{\mathbf{V{}'_1+Z_0I{}'_1}}{2\mathbf{\sqrt{Z_0}}}e^{-\gamma (-l_1)}e^{\gamma (-l_1)}\\ \end{bmatrix}\\ &= \begin{bmatrix} \frac{\mathbf{V_{1f}}}{\mathbf{\sqrt{Z_0}}}e^{-\gamma (-l_1)}\\ \frac{\mathbf{V_{1r}}}{\mathbf{\sqrt{Z_0}}}e^{\gamma (-l_1)}\\ \end{bmatrix}\\ &= \begin{bmatrix} a_1e^{j\beta l_1}\\ b_1e^{-j\beta l_1}\\ \end{bmatrix}\\ &= \begin{bmatrix} e^{j\beta l_1} & 0\\ 0 & e^{-j\beta l_1} \end{bmatrix} \begin{bmatrix} a_1\\ b_1\\ \end{bmatrix}\\ \begin{bmatrix} a{}'_2\\ b{}'_2\\ \end{bmatrix} &= \begin{bmatrix} \frac{\mathbf{V{}'_2+Z_0I{}'_2}}{2\mathbf{\sqrt{Z_0}}}\\ \frac{\mathbf{V{}'_2+Z_0I{}'_2}}{2\mathbf{\sqrt{Z_0}}}\\ \end{bmatrix}\\ &= \begin{bmatrix} \frac{\mathbf{V{}'_2+Z_0I{}'_2}}{2\mathbf{\sqrt{Z_0}}}e^{\gamma (-l_2)}e^{-\gamma (-l_2)}\\ \frac{\mathbf{V{}'_2+Z_0I{}'_2}}{2\mathbf{\sqrt{Z_0}}}e^{-\gamma (-l_2)}e^{\gamma (-l_2)}\\ \end{bmatrix}\\ &= \begin{bmatrix} \frac{\mathbf{V_{2f}}}{\mathbf{\sqrt{Z_0}}}e^{-\gamma (-l_2)}\\ \frac{\mathbf{V_{2r}}}{\mathbf{\sqrt{Z_0}}}e^{\gamma (-l_2)}\\ \end{bmatrix}\\ &= \begin{bmatrix} a_2e^{j\beta l_2}\\ b_2e^{-j\beta l_2}\\ \end{bmatrix}\\ &= \begin{bmatrix} e^{j\beta l_2} & 0\\ 0 & e^{-j\beta l_2} \end{bmatrix} \begin{bmatrix} a_2\\ b_2\\ \end{bmatrix}\\ \begin{bmatrix} b_1\\ b_2 \end{bmatrix} &= D \begin{bmatrix} b{}'_1\\ b{}'_2 \end{bmatrix} \\ \begin{bmatrix} a{}'_1\\ a{}'_2 \end{bmatrix} &= D \begin{bmatrix} a_1\\ a_2 \end{bmatrix}\\ D&=\begin{bmatrix} e^{j\beta l_1} & 0\\ 0 & e^{j\beta l_2} \end{bmatrix}\\ &=\begin{bmatrix} e^{j\delta _1} & 0\\ 0 & e^{j\delta _2} \end{bmatrix} \end{align*} $$ $$ \begin{align*} \begin{bmatrix} b{}'_1\\ b{}'_2 \end{bmatrix} &= \begin{bmatrix} S{}'_{11} & S{}'_{12}\\ S{}'_{21} & S{}'_{22} \end{bmatrix} \begin{bmatrix} a{}'_1\\ a{}'_2 \end{bmatrix}\\ \begin{bmatrix} b_1\\ b_2 \end{bmatrix} &= D \begin{bmatrix} b{}'_1\\ b{}'_2 \end{bmatrix} \\ &=D \begin{bmatrix} S{}'_{11} & S{}'_{12}\\ S{}'_{21} & S{}'_{22} \end{bmatrix} \begin{bmatrix} a{}'_1\\ a{}'_2 \end{bmatrix} \\ &=D \begin{bmatrix} S{}'_{11} & S{}'_{12}\\ S{}'_{21} & S{}'_{22} \end{bmatrix} D \begin{bmatrix} a_1\\ a_2 \end{bmatrix}\\ &=DS{}'D \begin{bmatrix} a_1\\ a_2 \end{bmatrix}\\ &=S \begin{bmatrix} a_1\\ a_2 \end{bmatrix}\\ \end{align*} $$ $$ \begin{align*} S&=DS{}'D\\ &= \begin{bmatrix} e^{j\delta _1} & 0\\ 0 & e^{j\delta _2} \end{bmatrix} \begin{bmatrix} S{}'_{11} & S{}'_{12}\\ S{}'_{21} & S{}'_{22} \end{bmatrix} \begin{bmatrix} e^{j\delta _1} & 0\\ 0 & e^{j\delta _2} \end{bmatrix}\\ &= \begin{bmatrix} e^{j\delta _1}S{}'_{11} & e^{j\delta _1}S{}'_{12}\\ e^{j\delta _2}S{}'_{21} & e^{j\delta _2}S{}'_{22} \end{bmatrix} \begin{bmatrix} e^{j\delta _1} & 0\\ 0 & e^{j\delta _2} \end{bmatrix}\\ &=\left [\begin{array}{ll} S{}'_{11}e^{2j\delta _1} & S{}'_{12}e^{j(\delta _1+\delta _2)}\\ S{}'_{21}e^{j(\delta _1+\delta _2)} & S{}'_{22}e^{2j\delta _2} \end{array} \right ] \end{align*} $$

參數轉換

$$ S=(\mathbf{Z}-\mathbf{Z_0}I)(\mathbf{Z}+\mathbf{Z_0}I)^{-1} $$

$$ \begin{align*} \mathbf{V}&=\begin{bmatrix}\mathbf{V_1}\\ \mathbf{V_2}\end{bmatrix}\: \mathbf{I}=\begin{bmatrix}\mathbf{I_1}\\ \mathbf{I_2}\end{bmatrix}\\ \mathbf{a}&=\begin{bmatrix}a_1\\ a_2\end{bmatrix}\: \mathbf{b}=\begin{bmatrix}b_1\\ b_2\end{bmatrix}\\ \mathbf{V} &= \mathbf{Z}\mathbf{I}\\ \mathbf{a}&=\frac{1}{2\sqrt{\mathbf{Z_0}}}(\mathbf{V}+\mathbf{Z_0I}) =\frac{1}{2\sqrt{\mathbf{Z_0}}}(\mathbf{Z}+\mathbf{Z_0}I)\mathbf{I}\\ \mathbf{b}&=\frac{1}{2\sqrt{\mathbf{Z_0}}}(\mathbf{V}-\mathbf{Z_0I}) =\frac{1}{2\sqrt{\mathbf{Z_0}}}(\mathbf{Z}-\mathbf{Z_0}I)\mathbf{I}\\ \frac{1}{2\sqrt{\mathbf{Z_0}}}\mathbf{I}&=(\mathbf{Z}+\mathbf{Z_0}I)^{-1}\mathbf{a}\\ \mathbf{b}&=\frac{1}{2\sqrt{\mathbf{Z_0}}}(\mathbf{Z}-\mathbf{Z_0}I)\mathbf{I}\\ &=(\mathbf{Z}-\mathbf{Z_0}I)(\mathbf{Z}+\mathbf{Z_0}I)^{-1}\mathbf{a}\\ &= S\mathbf{a} \end{align*} $$

即然可以從 \(\mathbf{Z}\) 轉換為 \(S\)，那麼 \(S\) 運用反矩陣也可以轉為 \(\mathbf{Z}\)
所以其他的參數也就可以轉換，可利用此篇的轉換表 [Circuit] Two-Port Networks 分析

範例

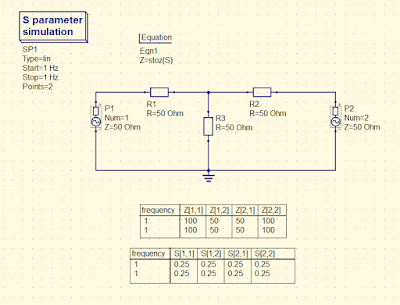
Qucs 自動

若 \(Z0\neq 50\Omega \)，stoz(S, Zref=50) 需更改 Zref 參數，預設為 50Ω

算式推導

$$ \begin{align*} S&=\begin{bmatrix} \mathbf{z_{11}}-\mathbf{Z_0} & \mathbf{z_{12}}\\ \mathbf{z_{21}} & \mathbf{z_{22}}-\mathbf{Z_0} \end{bmatrix} \begin{bmatrix} \mathbf{z_{11}}+\mathbf{Z_0} & \mathbf{z_{12}}\\ \mathbf{z_{21}} & \mathbf{z_{22}}+\mathbf{Z_0} \end{bmatrix}^{-1}\\ &=\begin{bmatrix} 50 & 50\\ 50 & 50 \end{bmatrix} \begin{bmatrix} 150 & 50\\ 50 & 150 \end{bmatrix}^{-1}\\ &=\begin{bmatrix} 50 & 50\\ 50 & 50 \end{bmatrix} \begin{bmatrix} \frac{3}{400} & \frac{-1}{400}\\ \frac{-1}{400} & \frac{3}{400} \end{bmatrix}\\ &=\begin{bmatrix} 0.25 & 0.25\\ 0.25 & 0.25 \end{bmatrix} \end{align*} $$

Qucs 手動
根據 Network Analyzer 原理，因 \(l_1=0\) 跟 \(l_2=0\)，故 \(S{}'=S\)
將 V2 Short，並將 RL_R 設為跟 Z0 一致，此時 a2 才會為 0，也才能求 S11 & S21
且此時 RL_L 的值無任何影響，沒有一定需為 Z0

將 V1 Short，並將 RL_L 設為跟 Z0 一致，此時 a1 才會為 0，也才能求 S12 & S22
且此時 RL_R 的值無任何影響，沒有一定需為 Z0

算式推導

$$ \begin{align*} S&=\begin{bmatrix} \mathbf{z_{11}}-\mathbf{Z_0} & \mathbf{z_{12}}\\ \mathbf{z_{21}} & \mathbf{z_{22}}-\mathbf{Z_0} \end{bmatrix} \begin{bmatrix} \mathbf{z_{11}}+\mathbf{Z_0} & \mathbf{z_{12}}\\ \mathbf{z_{21}} & \mathbf{z_{22}}+\mathbf{Z_0} \end{bmatrix}^{-1}\\ &=\begin{bmatrix} 25 & 50\\ 50 & 25 \end{bmatrix} \begin{bmatrix} 175 & 50\\ 50 & 175 \end{bmatrix}^{-1}\\ &=\begin{bmatrix} 25 & 50\\ 50 & 25 \end{bmatrix} \begin{bmatrix} \frac{7}{1125} & \frac{-2}{1125}\\ \frac{-2}{1125} & \frac{7}{1125} \end{bmatrix}\\ &=\begin{bmatrix} 0.0667 & 0.267\\ 0.267 & 0.0667 \end{bmatrix} \end{align*} $$

參考

Scattering parameters
S-Parameters
Reflection and Transmission
Transmission Lines
Multilayer Structures
RF Engineering Basic Concepts: S-Parameters S-parameter -- 基礎篇