[Circuit] Noise Factor & Noise Figure

電路知識：Noise Factor & Noise Figure

簡介：Noise Factor & Noise Figure 概念

Noise voltage
$$ V_n=\sqrt{4kTRB} $$ k = 波茲曼常數 \(1.38 \cdot 10^{-23} Joules/Kelvin\)
T = Temperature in Kelvin \(K= 273+°Celsius\)
R = 電阻阻值 \(\Omega\)
B = noise 頻寬 (Hz)

因熱攪動導致導體內部的電子達到平衡狀態時的電子雜訊，故與所施加電壓無關
等效電路如下

By Sbyrnes321 - Own work, CC0, Link

計算範例
一個 100kΩ 的電阻，在常溫 27℃ 加上一個 1MHz 頻寬的 noise
請問 Noise voltage 為何？
$$ \begin{align*} V_n &= \sqrt{4kTRB}\\ &= \sqrt{4\cdot 1.38\cdot 10^{-23}\cdot (273+27) \cdot 100 \cdot 10^3 \cdot 1\cdot 10^6}\\ &= 40.7uV\ \mathrm{RMS} \end{align*} $$

Noise Power
$$ \begin{align*} P&=kTB\\ P_{dBm}&=-174dBm+10log(B) (at\ 300K) \\ \end{align*} $$ k = 波茲曼常數 \(1.38 \cdot 10^{-23} Joules/Kelvin\)
T = Temperature in Kelvin \(K= 273+°Celsius\)
B = noise 頻寬 (Hz)

如下，因電阻匹配可得到最大 Noise Power，故令 \(R_{Load=R}\)
$$ \begin{align*} P_{Load}&=\frac{1}{2} \cdot \frac{V_n^2}{2R}\\ &=\frac{4kTRB}{4R}\\ &=kTB\\ \end{align*} $$

常溫 27℃ 下
$$ \begin{align*} P_{dBm}&=10log\frac{kTB}{1mW}\\ &=10log(\frac{1.38\cdot 10^{-23}\cdot 300 \cdot 1Hz}{1\cdot 10^{-3}})+10log(B)\\ &= -173.829dBm+10log(B)\\ &\approx -174dBm+10log(B) \end{align*} $$
計算範例
Ex. 1: 計算在常溫 27℃ 下，當 GSM 使用頻寬為 200kHz 時，請問其底噪是多少？
$$ -174dBM+10log(200\cdot 10^3)=-121dBm $$ Ex. 2: 計算在常溫 27℃ 下，當 SSB receiver 的頻寬為 2.4 kHz，請問其底噪是多少？
$$ -174dBM+10log(2.4\cdot 10^3)=-140dBm $$

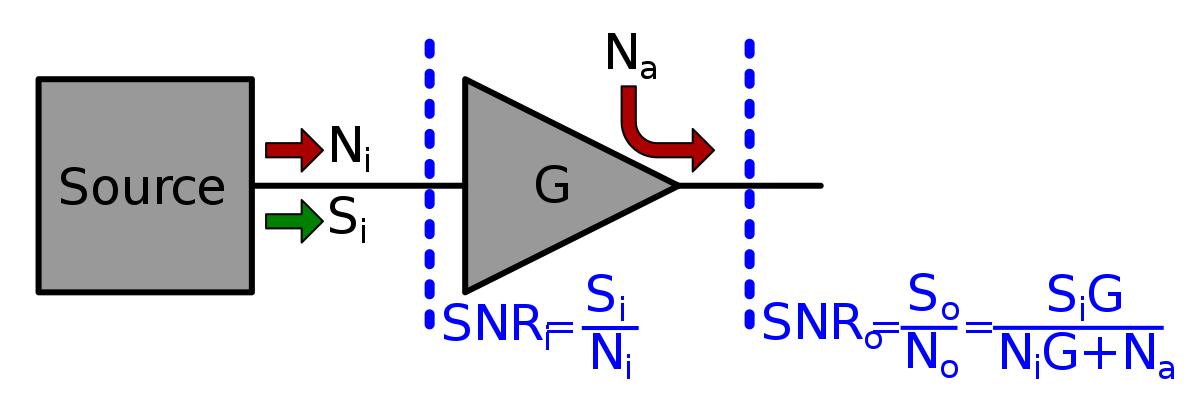
Noise Factor
$$ F=\frac{SNR_i}{SNR_o}=\frac{N_o}{N_iG}=1+\frac{N_a}{N_iG} $$ Noise Figure
$$ NF=10log(F) $$

其實就是 Output Noise 經過 AMP 後，增加了多少 AMP 內部的 Noise

By Fvultier - Using Inkscape, CC BY-SA 4.0, Link
$$ \begin{align*} F &= \frac{SNR_i}{SNR_o}\\ &= \frac{\frac{S_i}{N_i}}{\frac{S_o}{N_o}}\\ &= \frac{\frac{S_i}{N_i}}{\frac{S_iG}{N_o}}\\ &=\frac{N_o}{N_iG}\\ &=\frac{N_iG+N_a}{N_iG}\\ &=1+\frac{N_a}{N_iG}\\ \end{align*} $$
計算範例
請問經過此 AMP 後，Output Noise 為多少？

$$ -174dBm+10dB+3dB=-161dBm $$

Cascaded Noise Factor
$$ F_{total}=\frac{SNR_i}{SNR_o}=F_1+\frac{F_2-1}{G_1}+\frac{F_3-1}{G_1G_2} $$

By Fvultier - Using Inkscape, CC BY-SA 4.0, Link
$$ \begin{align*} F_{total}&=\frac{SNR_i}{SNR_o}\\ &= \frac{\frac{S_i}{N_i}}{\frac{S_o}{N_o}}\\ &= \frac{\frac{S_i}{N_i}}{\frac{S_iG_1G_2G_3}{N_iG_1G_2G_3+N_{a1}G_2G_3+N_{a2}G_3+N_{a3}}}\\ &=\frac{N_iG_1G_2G_3+N_{a1}G_2G_3+N_{a2}G_3+N_{a3}}{N_iG_1G_2G_3}\\ &= 1+\frac{N_{a1}}{N_iG_1}+\frac{N_{a2}}{N_iG_1G_2}+\frac{N_{a3}}{N_iG_1G_2G_3}\\ &= \underset{F_1}{\underbrace{1+\frac{N_{a1}}{N_iG_1}}}+\frac{1}{G_1}\underset{F_2-1}{\underbrace{\frac{N_{a2}}{N_iG_2}}}+\frac{1}{G_1G_2}\underset{F_3-1}{\underbrace{\frac{N_{a3}}{N_iG_3}}}\\ &= F_1+\frac{F_2-1}{G_1}+\frac{F_3-1}{G_1G_2} \end{align*} $$

參考

Noise figure Wiki
[通訊系統技術]-雜訊指數計算_Noise figure Calculation
Understanding Noise Figure
运算放大器噪声指数：不要被误导
Johnson–Nyquist noise
Friis formulas for noise